www.Papierfliegerei.de - Rechteckflieger - Teil 1

Es ist nicht schwer aus einem Blatt Papier einen Flieger mit annähernd rechteckiger Tragfläche zu bauen. Ken Blackburn zum Beispiel benutzte für seine Weltrekorde nur Papierflieger mit Rechtecktragfläche. Irgend etwas muss er aber besser machen als seine Nachahmer, sonst währe er nicht so lange Weltrekordhalter im Dauerflug geblieben. Es könnte sich also lohnen diese Fliegerform einer genaueren Untersuchung zu unterziehen.

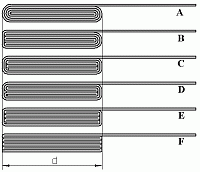Augenscheinlich benötigt ein Rechteckflieger mehrere Papierlagen als Ballast an der Spitze. Ken wickelt insgesamt 8 Lagen unter die Tragfläche. Aber man könnte die Lagen auch auf andere Arten unter die Tragfläche falten. Links ein par Beispiele (für eine größere Darstellung, wie immer, einfach das Bild anklicken). Die Blattdicke habe ich stark übertrieben, damit du das Knickmuster besser erkennen kannst. Ich bevorzuge übrigens die Variante B, da muß man nicht ganz so exakt falten können wie bei A. Es bleiben also folgende Fragen zu klären:

Sind 8 Lagen wirklich das Optimum für die Wulst an der Vorderkante?

Wie breit müssen die Papierlagen und wie groß muss die resultierende Flügeltiefe sein?

Das wollen wir hier untersuchen. Dazu müssen wir uns zuerst um den Schwerpunkt (Gravitation Center oder GC) des Fliegers kümmern. Ausgehen möchte ich von einem rechteckigem Blatt Papier mit der Breite B und der Höhe H. Ein Flieger aus so einem Blatt würde in etwas so aussehen.

Der Rumpf und die Flügelchen von Kens Flieger sind in unserer Darstellung noch nicht angelegt. Sie sind für Betachtungen um den Schwerpunkt unerheblich. Die Falttechnik der Frontwulst spielt ebenfalls eine untergeordnete Rolle, weil diese das Gewicht und den Schwerpunkt der Papierlagen in der Wulst nur unmerklich beeinflusst. Hauptsache die Wulst ist später schön flach, um den Luftwiederstand so gering wie möglich zu halten.

Den Schwerpunkt des Fliegers geben wir mit ks an. Dabei ist k ein Faktor und<0,5. Den genauen Wert werden wir etwas später bestimmen. Jetzt geht es uns erst mal um das allgemeine Festlegungen. Da Tragfläche und Wulst die selbe Breite haben, können wir auch diese bei unseren Überlegungen vernachlässigen. Zur Veranschaulichung habe ich noch die Flächenschwerpunkte der Wulst und der Tragfläche in unsere Skizze eingetragen. Statt mit der absoluten Dicke von Wulst und Tragfläche werden wir mit der Anzahl der Papierlagen rechnen. Schließlich lässt sich die Dicke nur Lagenweise verändern.

Stellen wir also das Liniengleichgewicht um GC auf. Wir erhalten:

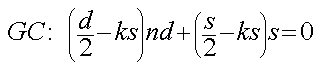
Außerdem kennen wir die Länge d der Wulst in Abhängigkeit von s und n:

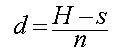
Setzen wir diese beiden Gleichungen ineinander ein, dann erhalten wir eine Quadratische Gleichung für s:

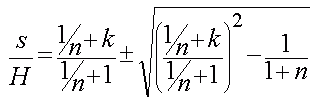
Unbekannt sind in dieser Gleichung noch k und n. Von n wissen wir das es eine Natürliche Zahl ungleich 0 sein muss. Da könnte man mit Probieren weiter kommen. Aber bei k hilft das nicht.
Am besten rechnest du ein par unterschiedliche Rechteckflügel mit den in meinem Buch hergeleiteten Formel durch, oder du benutzt meine kleine Exceltabelle. Versuche x_g so zu wählen, dass die Flugdauer maximal wird. Für alle denkbaren rechteckigen Tragflächen wirst du ein Verhältnis von x_g zu s von ungefähr 0,275 finden (x_g wird von der gewählten Flügelwölbung beeinflusst, deshalb variiert es leicht). Damit währ k bestimmt, denn k ist nichts anderes als genau dieses Verhältnis.

Gehen wir nun zurück zu unserer Bestimmungsgleichung für s. Imaginäre Lösungen sind für unser Problem uninteressant. Das bedeutet aber, dass die Wurzel der Gleichung größer 0 sein muss, damit wir den Flieger auch wirklich bauen können. Es muss also gelten:

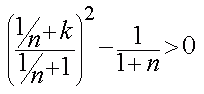
Setzen wir den eben gefundenen Wert für k ein und berücksichtigen das n eine Natürliche Zahl ist, dann ist diese Bedingung für n>5 erfüllt. Für einen flugtüchtigen Papierflieger benötigen wir demnach eine, mindestens aus 6 Lagen bestehende, Wulst an der Fliegerspitze.
Jetzt wird es interessant. Warum hat Kens Flieger 8 und nicht bloß 6 Lagen? Ein Flieger mit einer lediglich 6-lagigen Wulst müsste doch weniger Widerstand erzeugen als ein Flieger mit 8 Lagen an der Spitze. Ermitteln wir dazu erst einmal alle nach unseren Überlegungen möglichen Varianten von Rechteck-Fliegern. Ich höre hier bei n=10 auf, da dann die Wulst bei Verwendung von Kopierpapier sehr dick, hart und unhandlich wird und leicht bricht. Aber vielleicht sind mit anderem Papier 11 Lagen kein Problem, wer weiß? Wir untersuche hier jedoch nur ein Blatt Kopierpapier A4, welches wir hochkant halten (H=297 mm, B=210 mm, 80g/m²).

Wegen der Wurzel erhalten wir jeweils eine Doppellösung für s. Um die Tragfläche der neuen Flieger festzulegen müssen wir noch eine sinnvolle Annahme für die Spannweite treffen. Diese wird natürlich etwas kleiner als B ausfallen, weil ein Teil der Rumpffaltung und die hoch gestellten Flügelenden abgezogen werden müssen. Nehmen wir also beispielsweise folgendes an: Die Flügelenden währen ca. 10 mm hoch und der Rumpf 18 mm. Während des Fluges öffnete sich der Rumpf allerdings um ca. 11 mm. Damit hätten unser fiktiven Flieger eine, von Flügelende zu Flügelende gemessene, Spannweite b von:

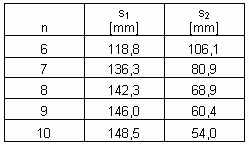
Außer der Flügeltiefe s und der Spannweite b können wir für jeden Flieger auch noch die Lage seines Schwerpunktes angeben (siehe nächste Tabelle).

Alles klar? Ich habe mir gleich noch eine schnittige Typenbezeichnung für die Flieger ausgedacht und die Flieger absteigend nach Flügeltiefe sortiert. Damit können wir jetzt die Fluggeschwindigkeit v und, für unseren Vergleich viel wichtiger, die minimal mögliche Sinkgeschwindigkeit u_min unserer Flieger errechnen. Die Flügelwölbung wollen wir hierzu vernachlässigen und ignorieren, dass wir uns dadurch etwas oberhalb des maximal zulässigen Anstellwickels bewegen. Dieses Vorgehen macht die Ergebnisse vergleichbarer, führt aber zu etwas überhöht berechneten Geschwindigkeiten. Am besten benutzt du wieder die Formeln aus meinem Buch. Wenn du mit meiner Exceltabelle rechnest, musst du die minimal mögliche Sinkgeschwindigkeit mittels des Gleitwinkels g aus der Fluggeschwindigkeit bestimmen:

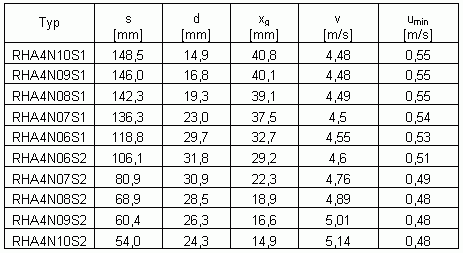Die um x_g, v und u_min erweiterte Tabelle sieht dann so aus:

Das ist ein doch ziemlich überraschendes Ergebnis. Obwohl die Tragfläche sich bei den einzelnen Varianten von oben nach unten auf fast 1/3 reduziert, steigt die Fluggeschwindigkeit nur mäßig an. Die minimale Sinkgeschwindigkeit reduziert sich sogar noch geringfügig. Anders als zu vermuten stellt Kens Flieger, in unserer Tabelle kommt die Variante RHA4N08S1 diesem am nächsten, nicht das aerodynamische Optimum dar. Aber die Varianten liegen auch so nahe beieinander, dass andere Kriterien von größerer Bedeutung sind.
Offensichtlich ist im Falle von rechteckigen Papierfliegern eine gute Beherrschbarkeit der Fliegerform wichtiger als das aerodynamische Optimum. Wir haben hier ja quasi ideale Papierflieger berechnet, ohne Rücksicht auf Herstellbarkeit, Formgenauigkeit und Festigkeit. Beispiele:

Je höher die Flügelstreckung ist desto eher neigen diese auf Grund der Wickelwulst zu Verwindungen. Dadurch können sich die Flugeigenschaften erheblich verschlechtern.

Papierflieger mit hoher Flügelstreckung lassen sich nicht so gut werfen und erreichen nicht die selben Starthöhen wie Flieger mit weniger Streckung.

Bei hoher Flügelstreckung werden die Rumpffalten stärker beansprucht, dadurch ist es schwieriger die Form des Fliegers im Flug vorauszubestimmen.

Der geringe aerodynamische Vorteil hoher Flügelstreckung kann diese Nachteile offensichtlich nicht ausgleichen. Ken hat ganz bewust die Fliegerform gewählt, welche bei gerade noch ausreichender Beherrschbarkeit der Wulst (8 Lagen sind ja schon ziemlich viel und die Unterschiede zu 9 und 10 Lagen sind wirklich minimal), die größte Tragfläche und damit die geringste Flügelstreckung hat. Mehr Wurfhöhe ist ihm offensichtlich wichtiger als eine mögliche geringere Sinkgeschwindigkeit. Trotzdem bleibt zu überlegen, ob ein Flieger mit 6 Lagen in der Wulst nicht besser ist. Die geringere Oberfläche reduziert schließlich den Luftwiderstand auch beim Werfen und die flachere Wulst trägt zusätzlich zur eine guten Wurfhöhe bei.

Können wir die Rechteckflieger damit abhaken? Nein, noch lange nicht! Drehen wir unser Ausgangsblatt A4 spaßeshalber um 90 Grad und nehmen es für die nächste Tabelle quer:

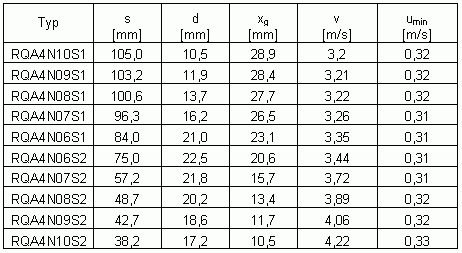Klar, die Spannweite ist jetzt mit ca. 252 mm wesentlich größer, dafür erhalten wir aber auch eine deutlich niedrigere minimale Sinkgeschwindigkeit. Erstaunlicher Weise zeigt sich diese sogar völlig unbeeindruckt von der gewählten Flügeltiefe. Wenn es dir gelingt einen Flieger der RQA4-Serie so hoch zu werfen wie die Flieger aus der RHA4-Reihe, dann ist dieser mit einiger Sicherheit mehr als 1,5 mal so lange in der Luft. Da sich nun Flieger mit niedriger Flügelstreckung besser werfen lassen als Flieger mit hoher Flügelstreckung (siehe oben), läuft es bei den Querfliegern auf die Variante RQA4N08S1 als bestmögliche hinaus.

Ha, acht Lagen unter dem Rumpf waren doch genau Kens Falttechnik! Nimmt er sein Papier etwa quer? Das ist durchaus möglich, wenn auch alle veröffentlichten Faltanleitungen seines Fliegers, zumindest die, welche mir bekannt sind, vom Hochformat ausgehen. Allerdings ist Ken ja Amerikaner und aus diesem Grund hat er wahrscheinlich sein Design nicht mit A4 sondern mit Papier im Letter-Format entwickelt. Um sicher zu gehen müsstest du also unsere keine Untersuchung noch einmal für einen Bogen Letter-Papier (216x279,5 mm) wiederholen.

Doch das ist immer noch nicht alles. Alle Flieger mit Mittelfalz haben ja eine fundamentale Schwäche, sie gehen in der Luft auf. Dadurch wird sowohl die richtige Flügelstellung als auch die Gleitflugtrimmung zu einem gewissen Grade dem Zufall überlassen. Der amtierende Weltmeister Takuo Toda verwendet hingegen eine Falttechnik, welche den Rumpf des Papierfliegers an der Spitze mittels eines Papierriegels schließt. Dadurch wird sein Flieger viel formstabiler, und genau das kannst du auch bei Rechteckfliegern erreichen. Wie du aber einen noch besseren Rechteckflieger baust, besprechen wir lieber auf <Rechteckflieger, Teil 2>.
Übrigens habe ich alle 20 hier vorgestellten Flieger gebaut und mit großen Erfolg probegeflogen. Wenn du es sebst auch versuchen willst, dann achte bitte unbedingt darauf, dass die Fliegerlänge s am Ende genau stimmt. Dazu ist es hilfreich, wenn du den ersten Falz mit etwas weniger als dem entgültigen d anlegst. Schließlich bleibt auch etwas Papier beim Umschlagen in den Knicken, je dicker die Wulst wird um so mehr.

www.Papierfliegerei.de - Rechteckflieger - Teil 1