www.Papierfliegerei.de - Rechteckflieger - Teil 2

Bei unseren Überlegungen zum Rechteckflieger haben wir bis jetzt einen wichtigen Aspekt völlig vernachlässigt. Das ist die Formstabilität des Fliegers.

Ken Blackburns Konstruktion öffnet sich im Flug, das heißt der Mittelfalz geht etwas auf und auch die Falze an den Flügelwurzeln geben nach. Dieses muss der Werfer im vorhinein richtig einschätzen und beim Einstellen des Papierfliegers berücksichtigen. Leider lässt sich das Öffnungsverhalten nicht gut vorhersagen. Neben den Beanspruchungen beim Abwurf gehen auch noch andere Faktoren mit ein. Zum Beispiel spielen Papiersorte und Orientierung sowie Luftfeuchtigkeit eine Rolle. Alles zusammen macht den perfekten Hochstart in den Gleitflug bis zu einem gewissen Grade zum Glücksspiel.

Mit einer ausreichend hohen Zahl an Modellen und Versuchen wirst du zwar nach der Wahrscheinlichkeitstheorie irgend wann mal einen erstklassigen Versuch hinbekommen, du wirst diese Leistung anschließend jedoch kaum wiederholen können.

Leider ist die Anzahl der Versuche bei den meisten offiziellen Wettbewerben und Veranstaltungen sehr begrenzt. Deshalb lohnt es sich über einen Papierflieger mit erhöhter Formstabilität nachzudenken. Zum Beispiel ist Takuo Todas Rekordflieger vorne mit einem Papierriegel verschlossen. Dieser hält den Mittelfalz zusammen und erhöht so die Formstabilität ganz bedeutend.

Nun lässt sich ein ähnlicher Riegel aber auch bei Rechteckfliegern anbringen. Das ist gar nicht so schwer wie du jetzt glaubst. Der erste, der meines Wissens eine solche Faltung vorgeschlagen hat, ist der Franzose Didier Boursin. Allerdings verwendet sein Entwurf eine quadratische Grundform und lediglich 3 Papierlagen Ballast unter der Tragfläche, und wir wissen ja bereits aus unseren früheren Überlegungen, das sind zu wenig für einen guten Flieger. Trotzdem ist die Falttechnik interessant, denn sowohl die Abmessungen des Ausgangsblattes als auch die Anzahl der Lagen in der Papierwulst lassen sich ja, wie ebenfalls schon gezeigt, leicht variieren. Nehmen wir also den <Looping> von Didier als Ausgangspunkt für unsere heutigen Betrachtungen.

Berechnen wir zuerst einmal wieder den Schwerpunkt des Papierfliegers. Dazu schneiden wir den Papierriegel an der Spitze in Gedanken durch und legen die Faltung flach vor uns.

Unser Ausgangsbogen soll wieder die Breite B und die Höhe H haben. Die Breite der Papierwulst ist d. Mit s bezeichnen wir wieder die Gesamttiefe des Fliegers und k ist wie gehabt der Faktor des Schwerpunktes (GC). Letztlich bleibt b als maximale Flügelbreite übrig, da 2d im Faltrumpf verschwinden (Beim Verwendung von Flügelendfalten müssen wir allerdings noch deren Höhe von b abziehen.). Wenn wir die Symmetrie berücksichtigen, gibt es drei Flächen mit einer jeweils unterschiedlichen Anzahl von Papierlagen, welche berücksichtigt werden müssen. (Ich habe in der Skizze auf das Eintragen der einzelnen Flächenschwerpunkte verzichtet um die Übersichtlichkeit nicht zu gefährden.) Demnach ergibt sich das Flächenmoment um GC zu:

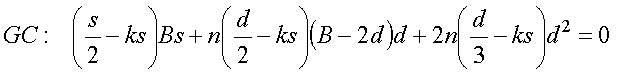
Außerdem gilt für die Wulstbreite d der selbe Zusammenhang wie beim letzten Mal, nämlich:

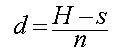
Setzen wir das in unsere Momentengleichung ein, so erhalten wir nach etwas Rechnerei eine Kubische Bestimmungsgleichung für s. In die Normalform gebracht sieht diese dann so aus:

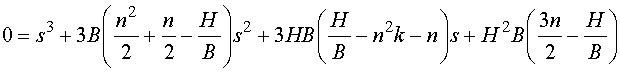
Die Konstante k hatten wir schon das letzte mal mit

angenähert. Damit lassen sich nun Lösungen für verschiedene Natürliche Zahlen n berechnen. Selbstverständlich ist auch das wieder ein bisschen mit Rechnerei verbunden. Darum empfiehlt es sich an dieser Stelle auch konkrete Werte für B und H einzusetzen und mit Zahlenwerten weiterzumachen. Da bietet sich als Ausgangsblatt wieder das Format A4 an. Um die Anzahl der möglichen Lösungen einzuschränken (und den Flieger am Ende auch wirklich bauen zu können) sollten wir noch bedenken, das für unser Problem nur Lösungen mit drei reellen Ergebnissen interessant sind. Das bedeutet das die Diskriminante der reduzierten Form kleiner Null sein muss (D<0). Falls du dich mit der Lösung von Kubischen Gleichungen schwer tust, findest du bei wiki unter <Cardanischen Formeln> Rat. Ober wende dich doch einfach an deinen Mathelehrer, der freut sich sicher ;-). 

Auch in diesem Fall lässt sich zeigen, dass mindestens 6 Papierlagen unter der Tragfläche benötigt werden. Es muss also wieder gelten n>5. Für Hoch- und Querformat erhalten wir diese Lösungen:

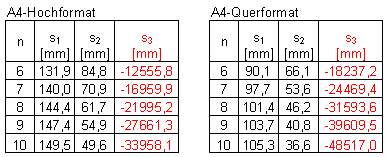Natürlich kann s nicht negativ werden. Deshalb entfallen für unser konkretes Problem auch die Lösungen s₃. Wir erhalten also wie beim letzten mal für jedes n eine Doppellösung. In den nächsten Tabellen habe ich die errechneten Varianten wieder um d, x_g (was ja nichts anderes als ks ist), b, v und u_min ergänzt. Das Vorgehen ist das selbe wie in <Rechteckflieger Teil1> beschrieben, darum spare ich mir hier die Erläuterung. Bei b habe ich noch je 10 mm für beide Flügelenden abgezogen. Somit erhalten wir:

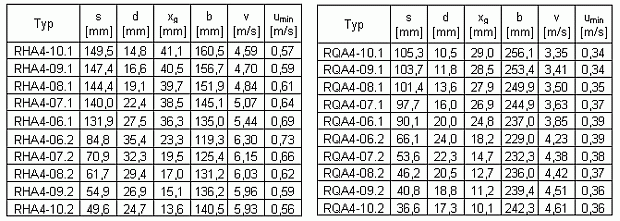
Ich bin sicher, dass du jetzt ein bisschen enttäuscht bist. Nach all der Mühe sind die errechneten Sinkgeschwindigkeiten, und nur auf diese kam es uns ja an, höher als bei vergleichbaren Fliegen nach Ken Blackburns Methode. Das liegt schlicht daran, dass sich der Faltrumpf jetzt nicht mehr öffnet und somit auch nicht zum Auftrieb beitragen kann. Wenn du aber genauer hinsiehst stellst du fest, für größere n werden die Unterschiede schnell kleiner. Allerdings nehmen mit n auch die Probleme beim Papierfliegerbau zu. Bei Verwendung von Papier mit 80 g/m², wie für die Tabellen vorausgesetzt, ist sinnvoll bei 8 Lagen Schluss. Dafür hast du dann aber auch einen sehr stabilen Papierflieger mit welchem sich ziemlich sicher gute Flüge machen lassen. Ich weiß das, weil ich auch diese Varianten alle probegeflogen habe.

Einen kleinen Makel hat die Falttechnik allerdings noch. Der Papierriegel verschließt nur die Spitze des Fliegers. Am hinteren Ende klafft der Rumpf gerne wieder auf. Um das zu verhindern musst du deinen Flieger entweder lange, mit einer Klammer verschlossen, lagern, sodass sich die Faltspannungen auswachsen können, oder du musst das hintere Ende mit einem Klebesteifen verschließen. Aber auch dafür gibt es Abhilfe. Hier zwei Papierflieger-Faltanleitungen, welche auf unseren heutigen Erkenntnissen basieren:

www.Papierfliegerei.de - Rechteckflieger - Teil 2